DataCook - Traitement de données PIRATA & Alimentation par Web-Service SOAP
Kevin Mambu, sous la direction de Nathalie Lefevre et Dimitry Khvorostyanov
Laboratoire LOCEAN, 2018
Introduction
Le programme expérimental PIRATA (Prediction and Research Moored Array in the Tropical Atlantic) est un programme de monitoring de la surface des océans dont la part est partagée entre le laboratoire LOCEAN (Laboratoire d’Océanographie et du Climat : Expérimentations et Approches Numériques) et la DT INSU (Division Technique de l’Institut National des Sciences de l’Univers du CNRS).
Des bouées munies de capteurs sont envoyées sur la surface d’océans pour une période d’un an, durant laquelle elles émettent leurs mesures par connexion satellite aux serveurs de l’entreprise CLS ARGOS, afin d’être ensuite traitées et examinées.
L’objectif de DataCook est de mettre à jour le dispositif de récupération et de traitement de données du protocole Telnet vers le le protocole SOAP via le WebService proposé par ARGOS.
Chaîne de communication
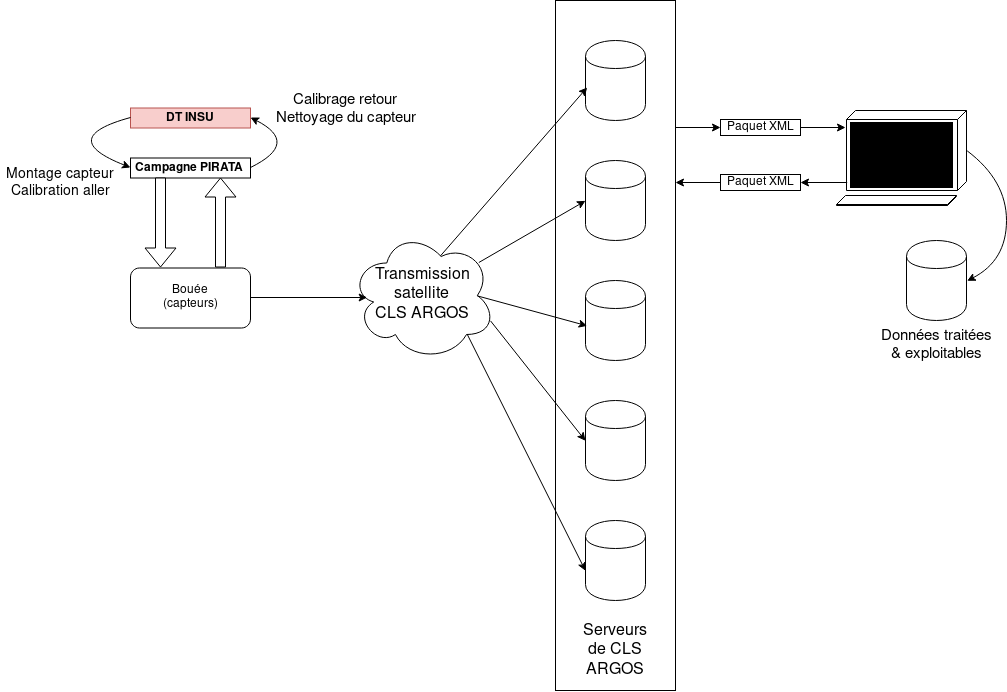 Les valeurs des capteurs sont émises par transmission satellites aux serveurs d’ARGOS sous le format d’une trame de données hexadécimales, d’une longueur de 184 bits (cf. annexe). Grâce au WebService SOAP fourni par CLS ARGOS, le client DataCook peut récupérer les données soous trois formes différentes :
Les valeurs des capteurs sont émises par transmission satellites aux serveurs d’ARGOS sous le format d’une trame de données hexadécimales, d’une longueur de 184 bits (cf. annexe). Grâce au WebService SOAP fourni par CLS ARGOS, le client DataCook peut récupérer les données soous trois formes différentes :
- Une liste des observations, préalablement tradutes par CLS Argos et serialisées au format XML.
- La même liste sérialisée au format CSV
- Une liste de passages de satellites, contenant chacun la trame de donnée brute dans une chaîne de caractères hexadécimaux.
Format de la requête SOAP
Le modèle de communication du protocole SOAP (Simple Object Access Protocol) est basé sur celui d’un échange de lettres entre le Client et le Serveur. Chaque parti doit en ce sens empaqueter sa requête / réponse dans une enveloppe formatée selon un certain format, dont la définition peut être retrouvée sur W3Schools. Les requêtes peuvent être des services élaborés sous forme de fonctions.
La précédente solution utilisait la fonction getStreamXml() pour récupérer les données brutes puis les passer ar une étape de décodage, mais il est préférable d’utiliser la fonction getObsXml() pour récupérer les observations pré-traduites (cf. Format de la réponse SOAP).
La librairie python Zeep permet de former ce genre de requête au serveur par le WebService fourni sans avoir à formater manuellement une enveloppe XML et en restant dans les paradigmes de programmation python.
Ainsi, notre appel à la fonction getObsXml() sera :
xml_str = client.service.getObsXml(username=user,password=pswd,platformId=pt_id,
nbDaysFromNow=1)
Format de la réponse SOAP
<DIST>
<PTT id="160637" program="3097" ptt_model="PMT RMF K" ptt_type="DRIFT">
<OBS id="147534467" latitude="-5.9998" loc_class="3" loc_date="2018-07-18T21:58:04Z" longitude="7.99044" obs_date="2018-07-19T00:00:00Z">
<LEVEL value="0.0">
<component element_name="DATA CO2 I596" value="4766.0"/>
<component element_name="DATA CO2 I810" value="7272.0"/>
<component element_name="BATTERY" value="10.679"/>
<component element_name="ATM PRESSION" value="1005.994"/>
<component element_name="HUMIDITY" value="50.5"/>
<component element_name="TEMP 02" value="23.31"/>
<component element_name="AIR SATURATION" value="94.5"/>
<component element_name="CONCENTRATION 02" value="251.55"/>
<component element_name="DATA CO2 TEMP" value="5278.0"/>
<component element_name="DATA CO2 LOW REF" value="4589.0"/>
<component element_name="DATA CO2 HIGH REF" value="3762.0"/>
<component element_name="DATA CO2 I434" value="2879.0"/>
</LEVEL>
</OBS>
<OBS>...</OBS>
</PTT>
<PTT>...</PTT>
</DIST>
nb : La syntaxe et le format est identique à la présentation des valeurs sur l’interface Web de CLS ARGOS.
Programmes et scripts
Les filtres sont omis pour cette section, cf la section suivante.
DataCook.py, principal module de manipulation des set d’observations au format CSV.convert_ascii.py, convertit un fichier reçu via Telnet au format CSV (assez lent à cause du parsing du fichier multiprocessing).convert_xls.py, convertit une feuille Excel contenant les observations au format CSV. Ces feuilles sont téléchargeables depuis l’interface Web de CLS Argos.fetch_soap.py, récupère les observations d’une bouée actuellement active via le protocole SOAP.generate_salinities.py, génère le set CSV ‘salinities’ en fonctio d’un fichier de mesures du taux de salinité passé en 2e paramètre.update_sqlite.py, met à jour la base de donnée SQLite3 pour l’application Web DataViewer.wp_generator.py, génère la page web d’un set d’observations particulier.
Filtrage et échantillonnage
Il n’est pas possible de garantir de tout temps l’exactitude des observations reçues depuis les serveurs de CLS Argos. En effet, la seule vérification qui est faite en amont de la réception de l’observation par transmission satellite est sur la bonne qualité de dite transmission. Mais les capteurs de la bouée peuvent être défaillants et transmettre, pour une observation à une date donnée, des mesures non représentatives de la réalité.
Ces données anormales doivent être filtrées, et pour cela plusieurs types de filtres ont été mis au point:
1) filter_mad.py (& filter_etalon.py), filtrage par ecart absolu médian “à la médiane” crénelé (Filtre intégré à la chaîne de données)
- L’écart absolu médian est en temps normal la moyenne des valeurs absolues de chaque écart à la médiane. Soit un ensemle de données de taille N, il est égal à .
- La variante dite “à la médiane” revient à calculer la médiane au lieu de la moyenne des écarts absolus à la médiane.

- Le filtrage se fait en prenant l’encadrement de cet écart à différents indices ( ou ) selon la Loi Empirique:
En statistique, la règle 68-95-99.7 (ou règle des trois sigmas ou règle empirique) indique que pour une loi normale, presque toutes les valeurs se situent dans un intervalle centré autour de la moyenne et dont les bornes se situent à 3 écarts-types de part et d’autre. Environ 68,27 % des valeurs se situent à un écart-type de la moyenne. De même, environ 95,45 % des valeurs se situent à 2 écarts-types de la moyenne. La quasi-totalité (99,73 %) des valeurs se situent à moins de 3 écarts-types de la moyenne.
En notation mathématique, ces faits peuvent être exprimés comme suit, où x est une observation d’une distribution normale d’une variable aléatoire, μ est la moyenne de la distribution, et σ est son écart-type :
- Ce filtrage est appliqué sur les variables suivantes : DATA_CO2_I810, DATA_CO2_TEMP, DATA_CO2_LOW_REF, DATA_CO2_HIGH_REF et ATM_PRESSION (la variante de test,
filter_etalon.py n’applique ce filtre que sur CO2_FUGACITE)
2) filter_static.py, filtrage par encadrements pré-déterminés
- Les fiches de calibration fournies par NKE comportent entre autres une série de bornes pour certains capteurs, qui servent à établir si la bouée est bien calibrée ou non (cf. Annexe). On peut alors filtrer le set d’observations en ne gardant que celles dont les mesures dites “significatives” sont correctement bornées. Ces mesures significatives sont celles intervenant dans le calcul de la fugacité du :
- DATA_CO2_I810
- DATA_CO2_LOW_REF
- DATA_CO2_HIGH_REF
- DATA_CO2_TEMP
- Certaines mesures ne sont pas formellement bornées par NKE, comme DATA_CO2_TEMP, et il faut faire appel à l’expertise d’un spécialiste pour établir une borne d’acceptation (dans notre cas, Mme Lefevre).
- cf Annexe pour les encadrements de calibration fournis par NKE.
- Pseudo-code:
i810_enc, refh_enc, refb_enc, temp_enc : encadrement
tmp : DataFrame
filter_std: fonction(dir: Lien_de_fichier)
dframe = Lire_total_param depuis dir
tmp.vider()
pour chaque ligne l de dframe:
si l['i810'] dans i810_enc
et l['refh'] dans refh_enc
et l['refb'] dans refb_enc
et l['co2_temp'] dans temp_enc:
tmp.enlever(l)
fin si
fin pour
pour chaque echantillon e de tmp.echantilloner_par('heure'):
tmp.aggreger(e, méthode='médiane')
fin pour
enregistrer(tmp)
fin fonction
3) filter_std.py, filtrage par encadrements des écarts-type
- Définition de Wikipedia :
En statistique, la règle 68-95-99.7 (ou règle des trois sigmas ou règle empirique) indique que pour une loi normale, presque toutes les valeurs se situent dans un intervalle centré autour de la moyenne et dont les bornes se situent à 3 écarts-types de part et d’autre. Environ 68,27 % des valeurs se situent à un écart-type de la moyenne. De même, environ 95,45 % des valeurs se situent à 2 écarts-types de la moyenne. La quasi-totalité (99,73 %) des valeurs se situent à moins de 3 écarts-types de la moyenne.
En notation mathématique, ces faits peuvent être exprimés comme suit, où x est une observation d’une distribution normale d’une variable aléatoire, μ est la moyenne de la distribution, et σ est son écart-type :
- L’idée est de considérer que la majorité des observations du set sont régulières et proches de la moyenne, tandis que les observations anormales le sont moins, on peut alors faire la même sélection que pour le filtre précédent, en remplaçant les bornes pré-déterminées par les encadrements de l’écart-type de chaque mesure significative.
- Les écarts-type et les moyennes sont, pour chaque mesure, calculés sur l’intégralité de la distribution.

- Sachant que la fugacité du est le résultat sur lequel se mesure la satisfaction du filtrage, il faut alors effectuer le filtrage des observations en fonction des mesures significatives (cf. filtrage précédent)
- En pratique, le programme génère trois set de données, chacun filtrés à un encadrement différent (, & ).
- Pseudo-code:
tmp : DataFrame
filter_std: fonction(dir: Lien_de_fichier)
dframe = Lire_total_param depuis dir
std_i810 = dframe['i810'].ecart-type()
std_refh = dframe['refh'].ecart-type()
std_refb = dframe['refb'].ecart-type()
std_temp = dframe['co2_temp'].ecart-type()
moy_i810 = dframe['i810'].moyenne()
moy_refh = dframe['refh'].moyenne()
moy_refb = dframe['refb'].moyenne()
moy_temp = dframe['co2_temp'].moyenne()
pour i allant de 1 à 3:
tmp.vider()
pour chaque ligne l de dframe:
si abs(moy_i810 - i*std_i810) >= l['i810']
et abs(moy_refh - i*std_refh) >= l['refh']
et abs(moy_refb - i*std_refb) >= l['refb']
et abs(moy_temp - i*std_temp) >= l['co2_temp']:
tmp.ajouter(l)
fin si
fin pour
pour chaque echantillon e de tmp.echantilloner_par('heure'):
tmp.aggreger(e, méthode='médiane')
fin pour
enregistrer(tmp)
fin pour
fin fonction
4) filter_fCO2.py, filtrage par encadrement de l’écart-type de la fugacité du
- Lors de ce filtrage, les observations éliminées sont celles dont la valeur de la fugacité du ne rentrent pas dans les encadrements de l’écart-type de cette dernière.
- Ce filtre est fait car la fugacité du est la grandeur physique au centre du projet PIRATA et, en ce sens, le résultat à privilégier.
- Les écarts-type et la moyenne sont, pour chaque mesure, calculés sur l’intégralité de la distribution.
- Pseudo-code:
tmp : DataFrame
filter_std: fonction(dir: Lien_de_fichier)
dframe = Lire_total_param depuis dir
std_fCO2 = dframe['fCO2'].ecart-type()
moy_fCO2 = dframe['fCO2'].moyenne()
tmp.vider()
pour chaque ligne l de dframe:
si abs(moy_fCO2 - i*std_fCO2) >= l['fCO2']
tmp.ajouter(l)
fin si
fin pour
pour chaque echantillon e de tmp.echantilloner_par('heure'):
tmp.aggreger(e, méthode='médiane')
fin pour
enregistrer(tmp)
fin fonction
Échantillonnage et aggregation
Le set d’observations final, exploité par les chercheurs, ne doivent posséder qu’une une observation par date donnée. Or, les protocoles de récupérations utilisés (Telnet, Excel & SOAP) retournent potentiellement plusieurs observations par heure. Il faut alors adopter une stratégie d’échantillonnage et d’aggregation des données par heure.
À l’heure actuelle, un resampling/aggregation par médiane est effectué à la fin de chaque filtrage. Ces opérations sont redondantes entre elles lors de plusieurs passages de filtres, mais cela n’altère pas le set de données de façon indésirable.
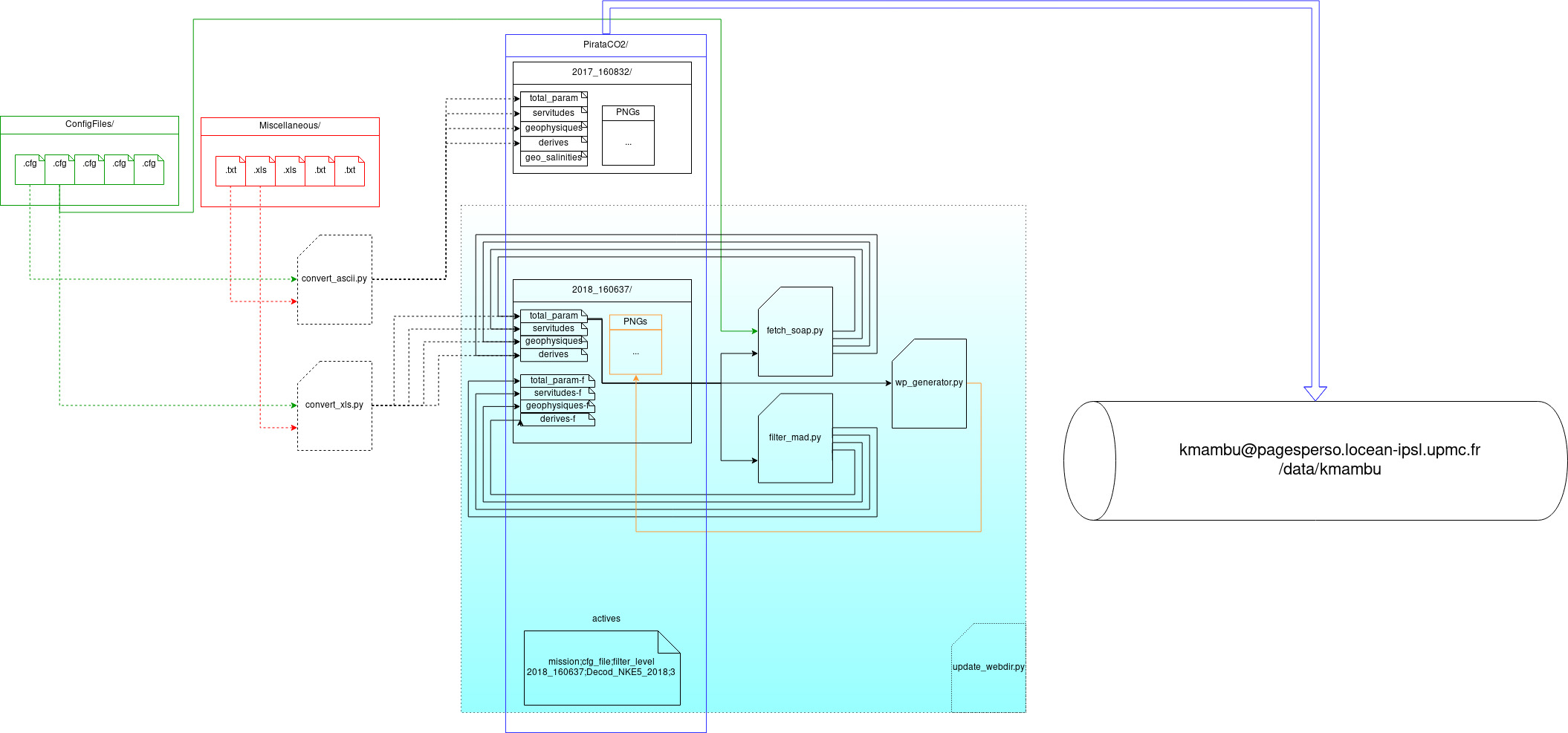
Chaîne de traitement de données de PIRATA
- Pour lancer les scripts Python, un mini-environnement conda est préparé. Ce dernier contient en particulier les modules suivants :
pandas, numpy & zeep, ce dernier n’étant installé sur la distribution Anaconda d’aucun serveur du laboratoire .
- À l’heure actuelle, le coeur de la chaîne de traitement de PIRATA est concentré dans le script python
update_webdir.py:
- Le script met à jour (récupération / filtrage / generation pages web) les dossiers qui figurent dans le fichier
actives. Ce fichier est à la racine du dossier Web (PirataCO2/)
cd DataCook
echo "[pirata] sourcing conda environment"
source /usr/home/kmambu/.conda/envs/pirata_env/bin/activate pirata_env
python ./update_webdir.py PirataCO2
echo "[pirata] ok"
echo "[pirata] updating pagesperso"
ssh depot-web """
cp -r ~/DataCook/index.html /data/kmambu;
cp -r ~/DataCook/Documentation /data/kmambu;
cp -r ~/DataCook/PirataCO2 /data/kmambu;
"""
echo "[pirata] ok"
echo "[pirata] git auto-update"
git pull
git add PirataCO2
git commit -m "[crontab] automatic update"
git push
echo "[pirata] done"
Fonctions de DataCook
computeFromFileRawData(date,hexStr,cfg_file) (obsolète)
Cette fonction prend en paramètre la trame hexadécimale sous la forme d’une chaîne de caractères et retourne un dictionnaire de toutes les variables de calculs asspost-traitement associées à leur valeur, calculées par le fichier de configuration cfg_file.
À la suite de cette documentation, ce format définit les tableaux contenants les données de capteurs (tableau de capteurs).
computeFromFileObsData(d,cfg_file)
Prend en paramètre un dictionnaire {sensor_name : value} et un fichier de configuration.
Retourne un dictionnaire des paramètre du CO2 : {'pCO2th':, 'fCO2':, 'Amax'}.
DataCook.computeFromFileTelnet(tab,cfg_file)
Prend en paramètre un tableau des valeurs des 15 capteurs et retourne un dictionnaire de toutes les variables de calculs associées à leur valeur, calculées via cfg_file.
Annexes
À l’intention des mainteneurs du programme.
Table de conversion des capteurs (à utiliser si ObsXml venait à cesser de fonctionner)
| sensor no. |
Parameter |
Number of bits |
Bits |
Min value |
Max value |
Default value |
Resol. |
Unit |
| 1 |
Checksum |
8 |
0-7 |
0(0) |
255(255) |
|
1 |
|
| 2 |
Heure de l’obsevation |
5 |
8-12 |
0(0) |
23(23) |
|
1 |
|
| 3 |
Minute de l’observation |
6 |
13-18 |
0(0) |
59(59) |
|
1 |
|
|
Partie aérienne |
|
|
|
|
|
|
|
| 4 |
Pression atmosphérique |
12 |
19-30 |
900(0) |
1100(4094) |
(4095) |
0.0488 |
|
| 5 |
Vbatt |
8 |
31-38 |
0(0) |
15(254) |
(255) |
0.059 |
|
|
Partie sous-marine |
|
|
|
|
|
|
|
| 6 |
Data :I810 |
13 |
39-51 |
0(0) |
8190(8190) |
(8191) |
|
|
| 7 |
Data :I596 |
13 |
52-64 |
0(0) |
8190(8190) |
(8191) |
|
|
| 8 |
Data :I434 |
13 |
65-77 |
0(0) |
8190(8190) |
(8191) |
|
|
| 9 |
Data : High Reference (1) |
6 |
78-83 |
3700(0) |
3762(62) |
(63) |
|
|
| 10 |
Data : Low Reference (1) |
6 |
84-89 |
4550(0) |
4612(62) |
(63) |
|
|
| 11 |
Data : Temperature (1) |
13 |
90 |
102 |
0(0) |
8191(8191) |
|
|
| 12 |
Concentration |
16 |
103-118 |
0(0) |
650(65000) |
(65535) |
0.01 |
|
| 13 |
Air saturation |
14 |
119-132 |
0(0) |
160(16000) |
(16383) |
0.01 |
|
| 14 |
Temperature |
12 |
133-144 |
-5(0) |
35(4000) |
(4095) |
0.01 |
|
| 15 |
Humidity |
8 |
145-152 |
0(0) |
127(254) |
(255) |
0.5 |
|
(1) : si val , alors soustraire 8192
Calculs des paramètres de
Les constantes de calculs suivantes sont dépendantes du modèle de la bouée dispatchée:
Veuillez regarder les tables de calibrations, dans la suite de l’annexe, pour les valeurs des constantes.
Température du au niveau de la mer (SST)
Pression du au niveau de la mer
Fugacité du
Tables de calibration
Ces feuilles de calibration permettent selon les modèles de bouées de correctement calibrer les spectrophotomètres.
NKE 6 (Mars 2017 / Mars 2018)
NKE 5 (Mars 2018 / Mars 2019)
Kevin Mambu, LIP6, Juillet 2018
 Les valeurs des capteurs sont émises par transmission satellites aux serveurs d’ARGOS sous le format d’une trame de données hexadécimales, d’une longueur de 184 bits (cf. annexe). Grâce au WebService SOAP fourni par CLS ARGOS, le client DataCook peut récupérer les données soous trois formes différentes :
Les valeurs des capteurs sont émises par transmission satellites aux serveurs d’ARGOS sous le format d’une trame de données hexadécimales, d’une longueur de 184 bits (cf. annexe). Grâce au WebService SOAP fourni par CLS ARGOS, le client DataCook peut récupérer les données soous trois formes différentes :